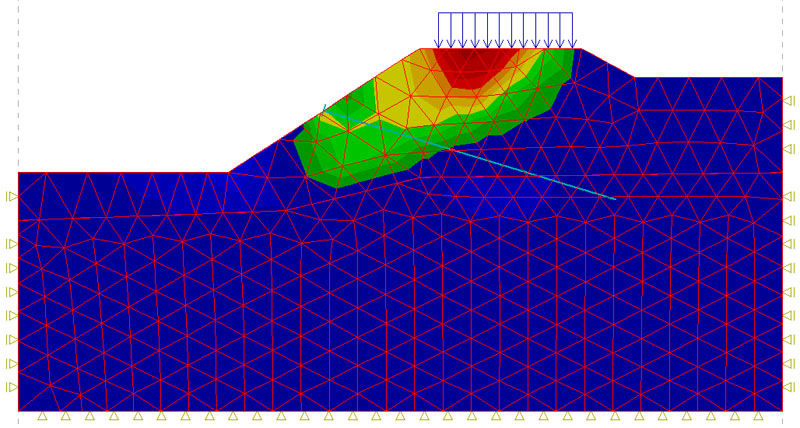
The finite element method

Data: 4.03.2018 / Rating: 4.6 / Views: 736

Gallery of Video:

Gallery of Images:

The finite element method - DOWNLOAD

The finite element method

PDEs and Finite Elements Version 10 extends its numerical differential equationsolving capabilities to include the finite element method. Given a PDE, a domain, and boundary conditions, the finite element solution process including grid and element generation is fully automated. [Table of Contents Basic Steps of the Finite Element Method As stated in the introduction, the finite element method is a numerical procedure for obtaining solutions to boundaryvalue problems. What are some good books to learn finite element analysis? What are the prerequisites for studying Finite Element Method or Finite Element Analysis? What is the use of finite element analysis. Kalman Filter Finite Element Method Applied to Dynamic Motion of Ground Kalman Filter Finite Element Method Applied to Dynamic Motion of Ground Yusuke KATO Department of. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis (Dover Civil and Mechanical Engineering) [Thomas J. FREE shipping on qualifying offers. This text is geared toward assisting engineering and physical science students in cultivating comprehensive skills in linear static and dynamic finite element methodology. the Finite Element Method, Third Edition, McGrawHill, New York, 2006. Computer solutions to certain problems of Chapter 8 (see Chapter 13 problems) are also included at the end of Chapter 8. The instructor should make an eort to review the problems before assigning them. The aim of this journal is to provide ideas and information involving the use of the finite element method and its variants, both in scientific Lecture Notes: The Finite Element Method Fall2013 Contents 1 6 FEM3DPACK is a MATLAB library which contains utility routines for 3D finite element calculations. Licensing: The computer code and data files described and made available on this web page are distributed under the GNU LGPL license. Finite element methods and solution procedures for linear and nonlinear analyses are presented using largely physical arguments. The homework and a term project (for graduate students) involve use of the general purpose finite element analysis program ADINA. NPTEL provides Elearning through online Web and Video courses various streams. Search for jobs related to Finite element method tutorial or hire on the world's largest freelancing marketplace with 14m jobs. It's free to sign up and bid on jobs. Finite element analysis (FEA) is a computerized method for predicting how a product reacts to realworld forces, vibration, heat, fluid flow, and other physical effects. Finite element analysis shows whether a product will break, wear out, or work the way it was designed. Source Mathematician Gilbert Strang on differential equations, history of finite elements, and problems of the method. Larson, Fredrik Bengzon The Finite Element Method: Theory, Implementation, and Practice November 9, 2010 Springer The finite element method is a powerful numerical analysis technique that has been widely applied in earthquake engineering for modeling the response of structures. The method derives its power from the variety of elements, such as beams, shells, and springs, that can be combined together to represent complex systems. Much of the success of the Finite Element Method as a computational framework lies in the rigor of its mathematical foundation, and this needs to be appreciated, even if. NPTEL provides Elearning through online Web and Video courses various streams. The finite element method (FEM) is a technique to solve partial differential equations numerically. It is important for at least two reasons. First, the FEM is able to solve PDEs on. The finite element method (FEM), or finite element analysis (FEA), is a computational technique used to obtain approximate solutions of boundary value problems in engineering. Boundary value problems are also called field problems. The field is the domain of interest and most often represents a physical Finite element method (FEM) is a numerical method for solving a differential or integral equation. It has been applied to a number of physical problems, where the governing differential equations are available. The method essentially consists of assuming the piecewise continuous The Finite Element Method: Its Basis and Fundamentals [Olek C Zienkiewicz, Robert L Taylor, J. FREE shipping on qualifying offers. The Finite Element Method: Its Basis and Fundamentals offers a complete introduction to the basis of the finite element method To the appropriate model, the wide range of devices in the electrical engineering fields, the finite element method (FEM) [3, 4 is a very useful technique, when the problems with complex geometry. The mixed finite element method is a type of finite element method in which extra independent variables are introduced as nodal variables during the discretization of a partial differential equation problem. Chapter 6 Finite Element Methods for 1D Boundary Value Problems The nite element (FE) method was developed to solve complicated problems in engineering, notably in elasticity and structural mechanics modeling involving el Finite Element Method January 12, 2004 Finite Element Method Boundary Element Method Finite Difference Method Finite Volume Method Meshless Method. DescriptionFEM cuts a structure into several elements (pieces of the structure). The finite element method is a systematic way to convert the functions in an infinite dimensional function space to first functions in a finite dimensional function space and then finally ordinary vectors (in a vector space) that are tractable with numerical methods. Browse and Download Finite Element Analysis books of various titles, written by many authors and published by a number of publications for free in PDF format. Download eBooks for free from Engineering study Material site. Finite element methods represent a powerful and general class of techniques for the approximate solution of partial dierential equations; the aim of this course is to provide an introduction to their mathematical theory, with special emphasis on The finite element method (FEM) is a powerful technique originally developed for numerical solution of complex problems in structural mechanics, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at discrete points called nodes. Description of the use of the finite element method to approximate a PDE solution using a piecewise linear function. Mathematics of Finite Element Method. Consider a second order differential equation in one dimension: with boundary conditions specified at x0 and x. The Finite Element Method for Problems in Physics from University of Michigan. This course is an introduction to the finite element method as applicable to a range of problems in physics and engineering sciences. Since finite element analysis is an applied science, gaining experience in analysis is extremely crucial for the effectiveness of results. You can best acheive this by examining the intermediate steps of the analysis carefully and performing lots of calculations with various loading and meshing conditions. The finite element method (FEM) is a numerical technique used to perform finite element analysis (FEA) of any given physical phenomenon. It is necessary to use mathematics to comprehensively understand and quantify any physical phenomena, such as structural or fluid behavior, thermal transport. The finite element method is one of the most powerful numerical methods available for solving partial differential equations; which apply over complex shapes The finite element method (FEM) is a numerical method for solving problems of engineering and mathematical physics. It is also referred to as finite element analysis (FEA). Typical problem areas of interest include structural analysis, heat transfer, fluid flow. Lectures on The Finite Element Method By Ph. Vanninathan Tata Institute of Fundamental Research Bombay 1975 The Finite Element Method Set, 7th Edition is an extensive reference resource covering the theory and application of FEM in solid, structural and fluid systems. The finite element method is a numerical analysis technique used by engineers, scientists, and mathematicians to obtain solutions to the differential equations that describe, or approximately describe a wide variety of physical (and nonphysical) problems. Physical problems range in diversity from. The finite element method (FEM) has developed into a key technology in the modelling and simulation of advanced engineering systems in various fields such as housing, transportation, and communications. The finite element analysis is the simulation of any given physical phenomenon using a numerical technique called finite element method (FEM). Engineers use this method to reduce the number of physical prototypes and experiments, and to optimize components in their design phase to develop better products, faster. Bathe KJ (2016) Finite Element Procedures. PE281 Finite Element Method Course Notes summarized by Tara LaForce Stanford, CA 23rd May 2006 1 Derivation of the Method In order to derive the fundamental concepts of FEM we will start by looking INTRODUCTION TO THE FINITE ELEMENT METHOD G. University of Aizu, AizuWakamatsu, Japan niki@uaizu. jp In the finite element method, Galerkin's method of weighted residuals is generally used. In this method, the governing partial differential equations are integrated over an element or volume after having been multiplied by a weight function. Reddy's An Introduction to the Finite Element Method, Third Edition, is an update of one of the most popular FEM textbooks available. The book retains its strong conceptual approach, clearly examining the mathematical underpinnings of FEM and providing a general approach to engineering application areas.

Related Images:

Similar articles:

....